Sinusfunktion und Kosinusfunktion

Die Sinus- und die Kosinusfunktion sind mathematische Funktionen, die sowohl

am rechtwinkligen Dreieck, als auch
in der Kreisgeometrie auftauchen (Trigonometrie am Einheitskreis).

Durch die Form ihrer Graphen spielen sie auch eine wichtige Rolle bei der mathematischen Beschreibung von Wellen und Schwingungen.

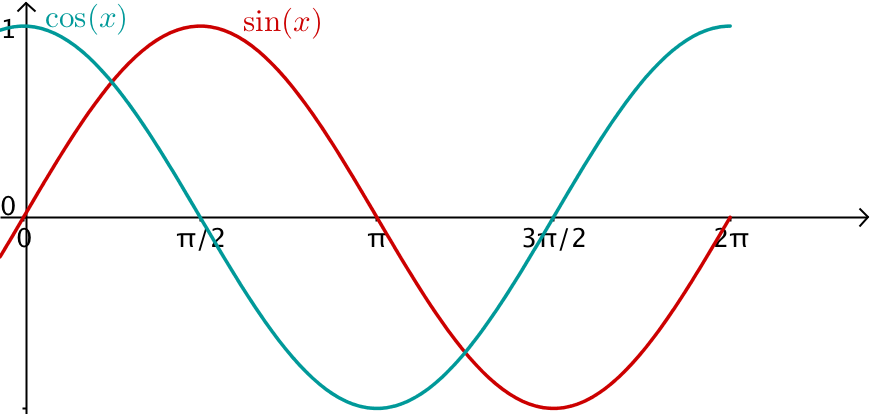
Eigenschaften

Der Sinus und der Kosinus haben beide

den gleichen Definitionsbereich (nämlich die reellen Zahlen)
den gleichen Wertebereich (das Intervall $[- 1,1]$ ) und sind beide
periodische Funktionen mit der Periode $2 π$ .

Außerdem ist der Sinus punktsymmetrisch zum Ursprung, und der Kosinus ist achsensymmetrisch zur y-Achse.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

	Sinus	Kosinus
Nullstellen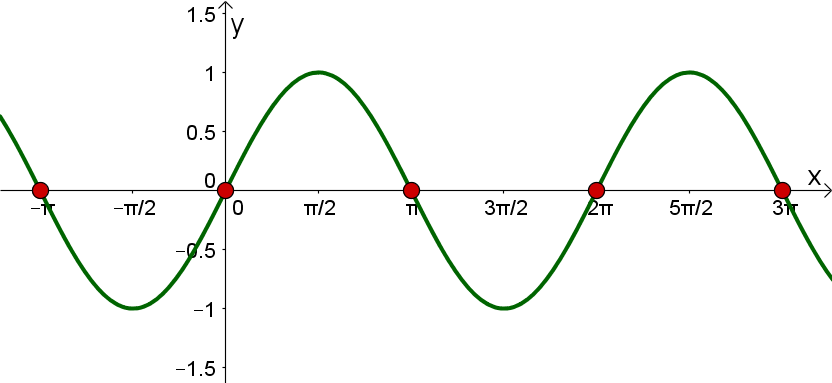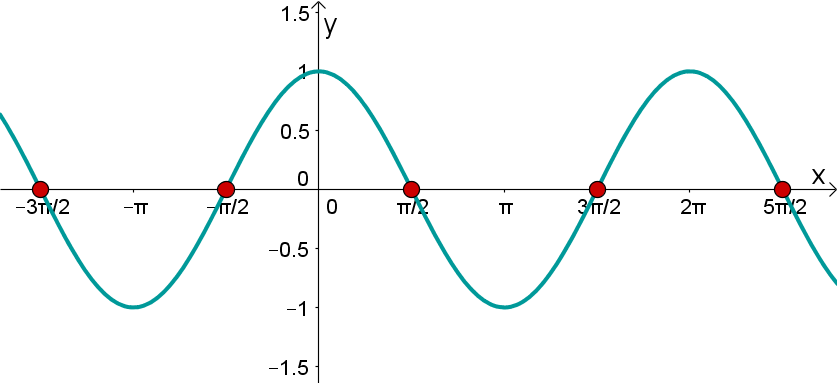
	Man sieht an den Schnittpunkten mit der x-Achse, dass für jedes $k \in ℤ$ gilt: $\sin (k \cdot π) = 0$ Das heißt $\to {\dots, - π, 0, π, 2 π, 3 π, \dots}$ sind die Nullstellen des Sinus.	Hier sieht man an den Schnittpunkten mit der x-Achse, dass für alle $k \in ℤ$ gilt: $c o s (\frac{π}{2} + k \cdot π) = 0$ Das heißt $\to {\dots, - \frac{π}{2}, \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, \dots}$ sind die Nullstellen vom Kosinus.
Extrema (max. und min.)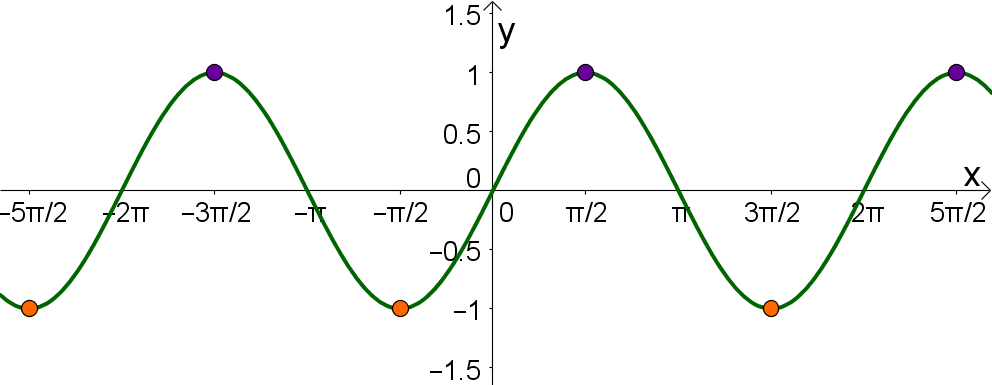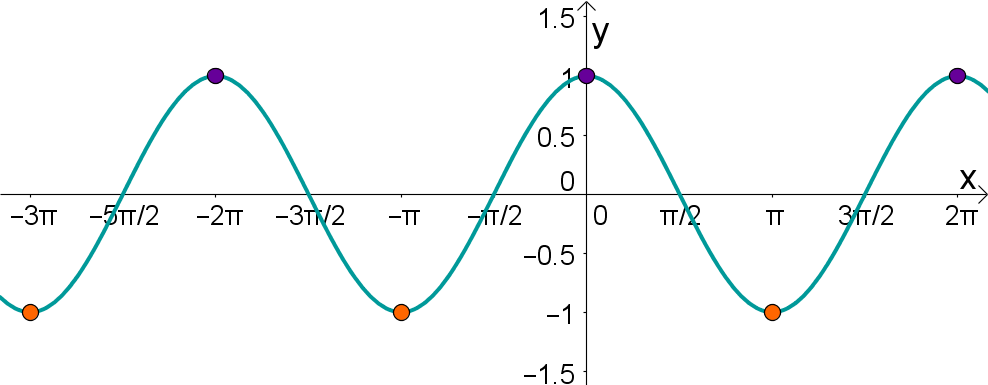
Extrema: Maximum	$\sin (\frac{4 k + 1}{2} \cdot π) = 1 f \ddot{u} r k \in ℤ$ , das heißt ${\dots, - \frac{7 π}{2}, - \frac{3 π}{2}, \frac{π}{2}, \frac{5 π}{2}, \frac{9 π}{2}, \dots}$ sind die Maxima vom Sinus.	$\cos (2 k \cdot π) = 1 mit k \in$ ℤ, das heißt ${\dots, - 4 π, - 2 π, 0,2 π, 4 π, \dots}$ sind die Maxima vom Kosinus.
Extrema: Minimum	$\sin (\frac{4 k - 1}{2} \cdot π) = - 1 f \ddot{u} r k \in ℤ$ das heißt ${\dots, - \frac{9 π}{2}, - \frac{5 π}{2}, - \frac{π}{2}, \frac{3 π}{2}, \frac{7 π}{2}, \dots}$ sind die Minima.	$\cos (2 k \cdot π + π) = - 1 mit k \in ℤ$ das heißt ${\dots, - 3 π, - π, π, 3 π, 5 π, \dots}$ sind die Minima.
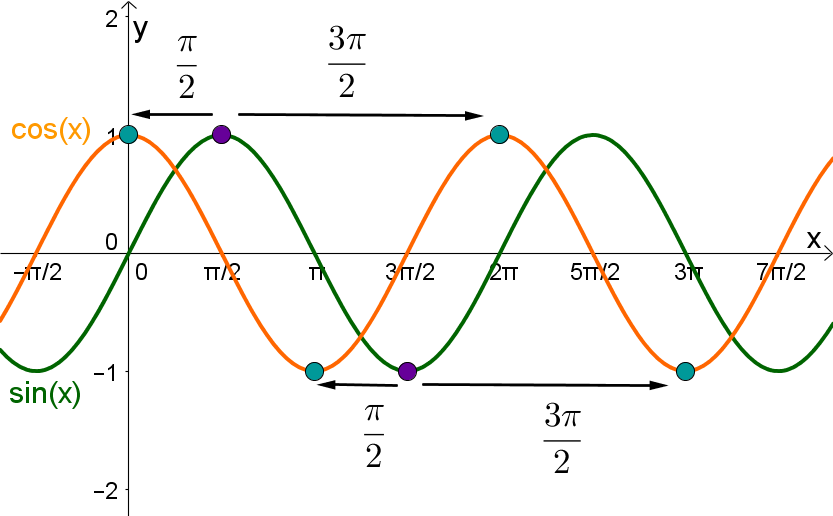
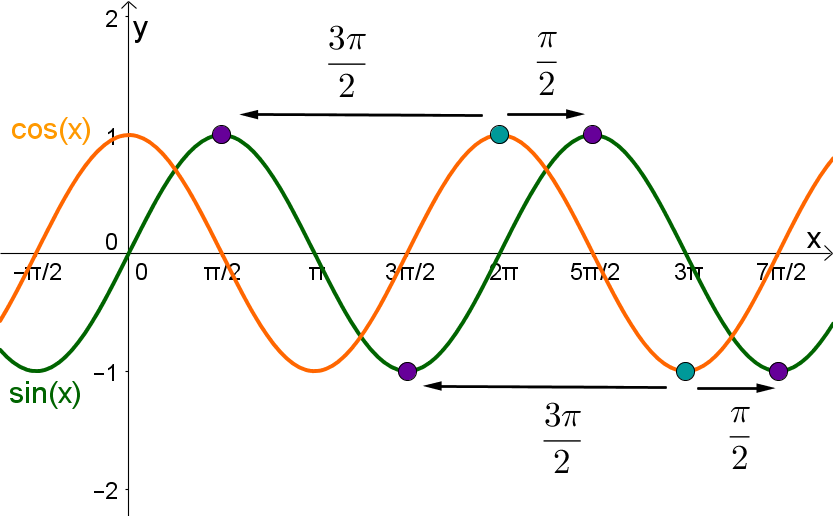
Zusammenhang zw. sin(x) und cos(x)	Wenn man den Graphen der Sinusfunktion um $\frac{π}{2}$ nach links oder um $\frac{3 π}{2}$ nach rechts verschiebt, ist er deckungsgleich mit dem Graphen der Kosinusfunktion. Das heißt $\sin (x + \frac{π}{2}) = \cos (x) = \sin (x - \frac{3 π}{2})$ .	Wenn man den Graphen der Kosinusfunktion um $\frac{3 π}{2}$ nach links oder um $\frac{π}{2}$ nach rechts verschiebt, ist er deckungsgleich mit dem Graphen der Sinusfunktion. Das heißt $\cos (x - \frac{π}{2}) = \sin (x) = \cos (x + \frac{3 π}{2})$ .

Beispielaufgaben

Skizziere die veränderte Sinusfunktion $f (x) = 2 \cdot \sin (x - \frac{π}{2})$ im Definitionsbereich $[- \frac{π}{2}, \frac{5 π}{2}]$ in ein Koordinatensystem und lies ihren Wertebereich, Nullstellen und Extremstellen ab.

Tipp: Im Artikel Verschieben und Strecken von trigonometrischen Funktionen findet man, was die $2$ vor dem sin und das $π / 2$ mit dem Graphen machen.

Lösung

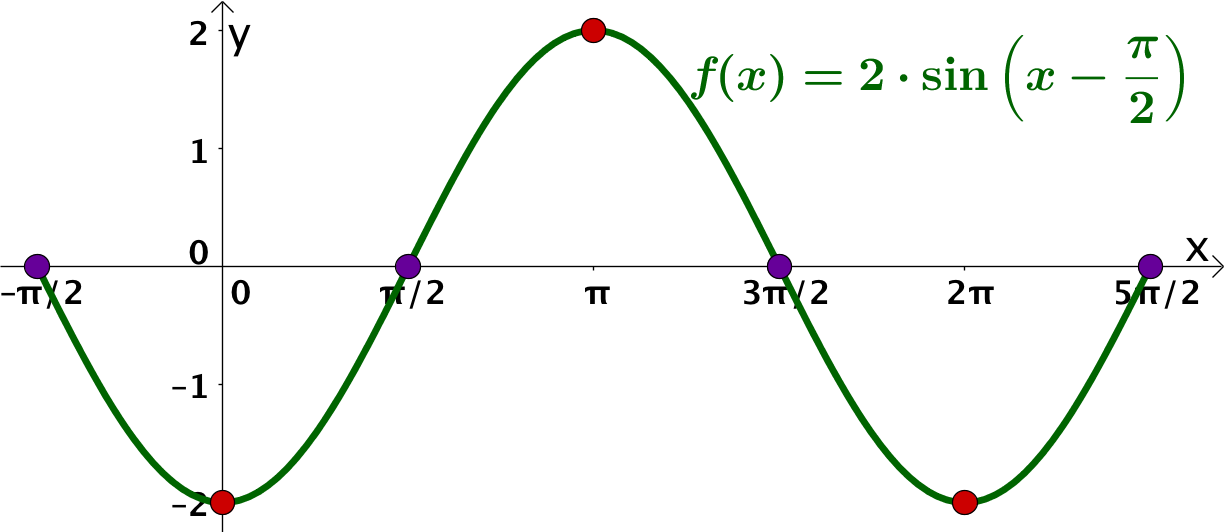
Hier hast du eine Sinusfunktion mit Amplitude $2$ , welche um $\frac{π}{2}$ nach rechts verschoben wurde.

Lies das Gesuchte aus dem Graphen ab.

Wertebereich: $[- 2,2]$

Nullstellen: $- \frac{π}{2}, \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}$